Effects of microcracks in brittle materials
Microcracks have a direct influence on the strength and thermoelastic properties of brittle materials such as ceramics. This microcrack network can result in an increase in light scattering, electrical and thermal resistance, and a decrease in the bulk coefficient of thermal expansion. The tunable material properties of microcracked ceramics provide a unique design opportunity. In order to utilize these materials, there is a need to understand the effect of mechanical loading on microcrack populations.
Microcracked Ceramic Metamaterials
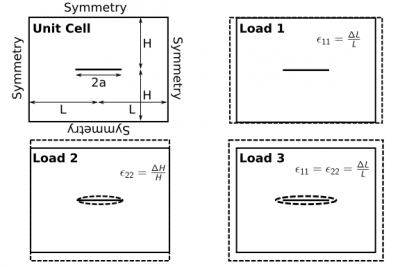
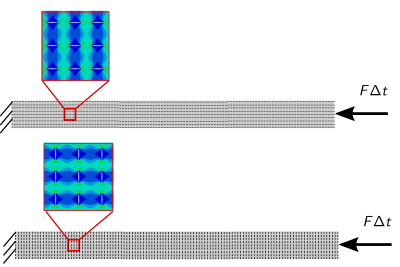
Microcrack density is a microstructural feature on contributing to nonlinear elastic and inelastic properties of brittle materials. We aim to engineer microcracked ceramic metamaterials. By optimizing the size, orientation, and density of microcracks in an elastic material there are possibilities for auxetic (negative Poisson’s ratio), increased strain tolerance, and increased thermal shock resistance metamaterials. Below is an example of guiding mechanical waves parallel and perpendicular to microcrack arrays.
Predicting Failure in two dimensional films like MoS2 and graphene
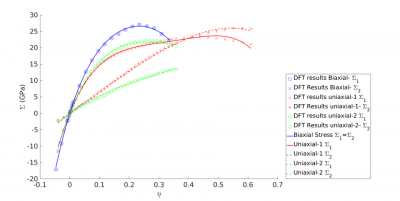
Calculating elastic constants of MoS2
Data calculated from VASP is compiled in 3 csv files for MoS2 with a unit cell of one Mo and 2 S atoms and interplanar spacing of 61.5 A.
The data is used in a least-squares curve fit based upon the 5th-order elastic energy expansion Cooper et al. 2014. Below is an example of running the code to generate these constants and plot the resulting stress-strain curves:
[Sx,Sy,ex,ey]=prepare_data('biaxial_data.csv','strain_x.csv','strain_y.csv');
C=elastic_constants(Sx,Sy,ex,ey,1);
C11= 223.1; C12= 68.9;
D111=-1871.7; D222=-1536.7; D112= -60.6;
E1111=11005.4; E1112= 372.6; E2222=5850.2; E1122= 13.3;
F11111=-31958.0; F11112=-3406.6; F11122=-1308.4; F12222=-11872.6;
F22222=-7501.6;